Data Structures and Algorithms

Videos #

• Abdul Bari’s Algorithms (84 videos) - Great teacher, who walks you through concepts end-to-end. Videos 19 - 29 (Recurrence Relations) can safely be skipped. If there were any DS / Algo topics you never thoroughly understood, definitely recommend looking it up here and giving it a watch.

Time Complexity #

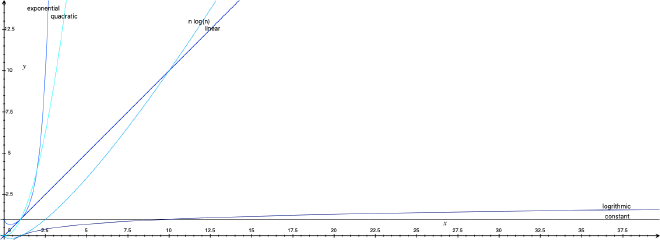
Ordering of complexities:
constant < logrithmic < linear < quadratic < cubic < exponential
\(1 < \log n < \sqrt{n} < n < n \cdot \log n < n^2 < n^3 < \ldots < 2^n < 3^n < \ldots < n^n \)

• Constant - \(O(1)\) - Takes the same amount of time, regardless of input size
  • get the first element of an array
  • pop the last element off of a stack
• Logrithmic - \(O(\log n)\) - Time taken increases very slowly as compared to input size increases
  • height of a balanced binary tree
  • binary search
• Linear - \(O(n)\) - Input size and time taken increases at the same rate
  • iterate on every item in an array
• Quadratic - \(O(n^2)\) - Time taken increases faster than growth in input size
• Cubic - \(O(n^3)\) - Time taken increases much faster than growth in input size
• Exponential - Time taken explodes with tiny increases in input size
  • \(O(2^n)\)
  • \(O(3^n)\)
  • \(O(n^n)\)

Loop	Big O Time	Notes
for (i=0; i<n; i++) {}	\(O(\log n)\)	Normal loop operating on every element once takes linear time
for (i=0; i<n; i+2) {}	\(O(\log n)\)	Skipping every other number is still linear time, because as the input grows, the time take still grows at a linear rate
for (i=n; i>1; i--) {}	\(O(\log n)\)	Normal loop going in reverse is still linear
for (i=0; i<n; i*2) {}	\(O(\log_2 n)\)	Multiplying by 2 reduces the number of times going through the loop, making it logrithmic (base 2)
for (i=0; i<n; i*3) {}	\(O(\log_3 n)\)	Similar to the above, except in this case it would be logrithmic (base 3)
for (i=n; i>1; i/2) {}	\(O(\log_2 n)\)	Similarly, dividing reduces the number of times the loop is called, making this logrithmic (base 2